Contoh Soal Nilai Mutlak Lengkap dengan Pengertian, Sifat, dan Penerapannya

Sebenarnya, ada banyak sekali contoh soal nilai mutlak dalam kehidupan sehari. Penggunaan yang paling umum dapat didefinisikan dengan konsep persamaan nilai mutlak linear satu variabel.

Dalam konsep linear ini, terdapat dua macam penerapan yang perlu kamu pahami. Yang pertama, fungsi persamaan. Dan yang kedua, fungsi pertidaksamaan. Namun, dalam tulisan ini, kita akan membahas fungsi persamaan terlebih dahulu.

Nah, untuk memahami persamaan nilai mutlak dengan lebih baik, simak pembahasan contoh soal nilai mutlak di bawah ini ya, Sobat Pijar!

Baca juga: Program Linear, Pengertian Model Matematika, dan Contoh Soalnya

Apa itu Persamaan Nilai Mutlak?

Sebelum membahas lebih jauh mengenai contoh soal nilai mutlak, kamu harus memahami dulu definisi persamaan nilai mutlak. Mudahnya, nilai mutlak dapat didefinisikan sebagai jarak angka dari titik nol pada garis angka. Jadi, dalam menentukan nilai mutlak, kamu bisa mengabaikan arahnya.

Jadi, ketika disebutkan kalau $|x| = 5$ , maka ada dua solusi yang bisa menjadi jawaban. Pertama, $x = 5$ dan yang kedua, $x = -5$. Supaya lebih mudah, kamu bisa menggunakan garis bilangan untuk menjawab contoh soal nilai mutlak ini. Misalnya, perhatikan garis bilangan berikut ini:

Dari gambar tersebut, kamu bisa melihat kalau titik –5 ataupun 5 sama-sama memiliki jarak 5 satuan dari titik nol. Sehingga, $x = -5$ ataupun $x = 5$ sama-sama memenuhi $|x| = 5$ .

Apa saja Sifat-Sifat Persamaan Nilai Mutlak?

Selain pengertian persamaan nilai mutlak, contoh soal nilai mutlak juga dapat dipecahkan dengan memahami sifat persamaan nilai mutlak linear satu variabel. Setidaknya, ada 3 persamaan umum yang paling sering digunakan untuk menjawab contoh soal nilai mutlak yang melibatkan persamaan nilai mutlak, yaitu:

1. $|x| = \sqrt{x^2}$

Dalam definisi sifat persamaan nilai mutlak ini, hasil dari $\sqrt{x^2}$ adalah $x$ . Sebagai gambaran, kalau kamu mencari jawaban dari $\sqrt{25}$ , hasilnya adalah $|5|$ . Hal ini karena baik $5^2$ atau $-(5)^2$ sama-sama menghasilkan angka 25. Sehingga, bisa dikatakan kalau $|x| = \sqrt{x^2}$ .

2. $|a.b| = |a|.|b|$

Untuk mendapatkan nilai mutlak dari perkalian dua bilangan, kamu bisa mengalikan dua bilangan tersebut lebih dahulu, kemudian mengalikannya. Atau dengan mencari nilai mutlak dari masing-masing bilangan, kemudian mengalikan nilai mutlaknya.

Agar lebih jelas, kamu bisa menggunakan contoh soal nilai mutlak ini sebagai gambaran. Misalnya, diketahui kalau $a=5$ dan $b=-4$ , dan kamu ingin mencari nilai mutlak hasil perkalian a dan b. Tidak masalah kalau kamu menghitungnya dengan cara $|5 . (-4)|$ atau $|5|.|(-4)|$. Cara manapun yang kamu pilih, keduanya akan sama-sama menghasilkan nilai 20.

3. $|\frac{a}{b}| = \frac{|a|}{|b|}, b\neq 0$

Hal yang sama juga berlaku saat akan mencari nilai mutlak dari pembagian dua bilangan. Kamu bisa membagi dua bilangan tersebut lebih dulu, kemudian mengubahnya menjadi bentuk nilai mutlak. Atau kamu bisa mengubah bilangan tersebut menjadi nilai mutlaknya terlebih dahulu sebelum melakukan pembagian.

Akan tetapi, sifat ini hanya berlaku apabila nilai b dalam contoh soal nilai mutlak tidak sama dengan nol.

Apa Sifat Perkalian Persamaan Nilai Mutlak?

Sifat perkalian nilai mutlak adalah salah satu contoh soal nilai mutlak dalam sifat persamaannya. Seperti yang sudah dibahas sebelumnya, sifat perkalian ini dapat dijabarkan dalam bentuk rumus:

$|a.b| = |a|.|b|$

Artinya, kalau kamu memiliki dua bilangan a dan b, maka nilai mutlak dari perkalian a dan b akan sama hasilnya dengan hasil kali nilai mutlak dari a dan nilai mutlak dari b. Sifat perkalian tersebut dapat berlaku untuk sembarang konstanta a. 

Bagaimana Penerapan Persamaan Nilai Mutlak?

Persamaan dan contoh soal nilai mutlak adalah salah satu persamaan matematika yang paling sering diterapkan dalam kehidupan sehari-hari. Berikut ini adalah beberapa contoh soal nilai mutlak dalam penerapan sehari-hari:

1. Menentukan Jarak

Penerapan contoh soal nilai mutlak cukup sering digunakan dalam menentukan jarak atau perbedaan antar dua bilangan. Misalnya, kamu ingin mencari tahu jarak antara 2 dan 5, maka kamu bisa menggunakan persamaan nilai mutlak satu variabel.

Caranya adalah dengan mencari nilai dari $|2-5|$. Dengan menggunakan persamaan nilai mutlak akan diketahui kalau hasil dari $|2-5|=|-3|$. Sehingga, jarak antara 2 dan 5 adalah 3. Nilai negatif bisa diabaikan karena dalam perhitungan jarak, arah bisa diabaikan.

2. Mencari Solusi Persamaan

Selanjutnya, contoh penerapan persamaan nilai mutlak dalam kehidupan sehari hari juga dapat digunakan untuk membantu menemukan solusi dari persamaan yang memiliki bilangan negatif. Misalnya, untuk mencari nilai $x$ dalam persamaan nilai mutlak $2x-3=5$. 

Persamaan ini dapat dituliskan juga sebagai $|2x-3| = 5$. Dalam persamaan tersebut, ada dua solusi yang bisa kamu dapatkan. Yaitu $x=4$ dan $x=-1$, tergantung dari nilai $|2x-3|$ adalah negatif atau positif.

3. Memecahkan Masalah Geometri

Persamaan nilai mutlak juga dapat digunakan untuk memecahkan masalah geometri. Salah satu contoh soal nilai mutlak dalam masalah geometri dapat digunakan untuk menentukan panjang sisi segitiga dalam koordinat kartesius.

Sebagai contoh, kamu mengetahui kalau sebuah segitiga ABC memiliki titik A di koordinat (2, 3) dan titik B di koordinat (5, 7). Maka, kamu bisa menentukan panjang sisi AV dengan menggunakan rumus jarak nilai mutlak. Sehingga, ditemukan kalau $|AB| = \sqrt{((5-2)^2 + (7+3)^2)} = \sqrt{34}$ .

4. Menghitung Nilai Rata-Rata

Contoh soal nilai mutlak juga bisa digunakan untuk menghitung nilai rata-rata dari sekelompok bilangan. Misalnya untuk menghitung nilai rata-rata mutlak. Untuk menghitung nilai rata-rata mutlak, kamu bisa menggunakan definisi matematika $\frac{(|a1|+|a2|+|an|)}{n}$ .

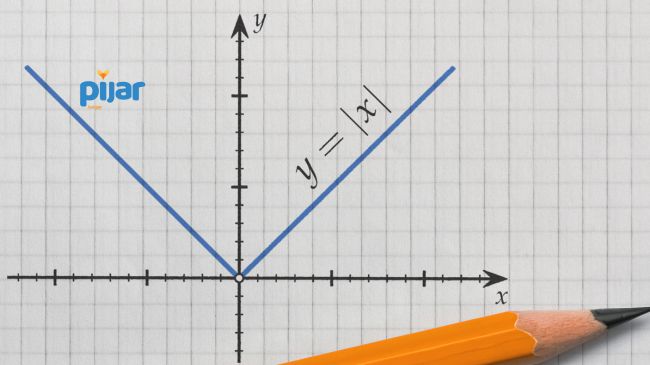
5. Membuat Fungsi Matematika

Kamu juga bisa menggunakan persamaan nilai mutlak untuk membuat fungsi matematika. Misalnya untuk menjawab contoh soal nilai mutlak ketika diketahui fungsi $f(x) = |x-2|+3$. Dari fungsi ini, kamu bisa mengetahui kalau fungsi tersebut memiliki garis tengah vertikal pada $x=2$ dan garis konstan $y=3$.

Jika digambarkan, fungsi dari contoh soal nilai mutlak ini akan membentuk grafik fungsi berupa V terbalik dengan titik puncak pada titik (2, 3).

Penerapan konsep dan contoh soal nilai mutlak tentu saja tidak terbatas pada contoh yang sudah disebutkan tadi. Ada banyak manfaat dan penerapan lain yang menggunakan konsep nilai mutlak. Kalau kamu berminat mendalami ilmu fisika, teknik, atau ekonomi, kamu akan menemukan lebih banyak lagi penerapan dan contoh soal nilai mutlak.

Contoh Soal Persamaan Nilai Mutlak

Agar lebih memahami persamaan nilai mutlak linear satu variabel, kamu bisa mengerjakan dan memperhatikan pembahasan contoh soal nilai mutlak kelas 10 berikut ini:

Contoh Soal Nilai Multak 1

Berdasarkan salah satu sifat nilai mutlak, selesaikan persamaan nilai mutlak linear satu variabel dari $|2x-1|=7$ .

Pembahasan:

Pembahasan untuk contoh soal nilai mutlak ini sebenarnya cukup sederhana. Untuk menyelesaikan persamaan tersebut, kamu bisa menggunakan sifat nilai mutlak $|x| = \sqrt{x^2}$.

Sehingga,

$\sqrt{(2x -1)^2} = 7$

$(\sqrt{(2x -1)^2})^2 = 7^2$

$(2x - 1)^{2} = 7^2$

$4x^2 = 4x +1 = 49$

$4x^2 - 4x - 48 = 0$

Kemudian, bagi semua ruas dengan 4. Sehingga diperoleh persamaan berikut:

$x^2-x-12=0$

$(x-4) (x+3)=0$

Sehingga, diperoleh hasil $x=4$ dan $x=-3$ .

Contoh Soal Nilai Mutlak 2

Contoh soal nilai mutlak berikutnya adalah tentang jarak. Misalnya, kamu ingin main ke rumah salah seorang teman bernama Raya setelah pulang sekolah. Selain itu, kamu juga ingin mampir membeli buku. Tapi kamu lupa dimana letak toko bukunya. Kemudian, kamu ingat kalau Raya pernah bilang jarak sekolah ke rumahnya adalah 5 km. Dan memang ada sebuah toko buku dengan jarak 1 km dari rumahnya. Tapi, berapa jarak toko buku tersebut kalau dihitung dari sekolah?

Pembahasan:

Agar lebih jelas, kamu bisa membuat ilustrasi atau gambar dari informasi yang sudah diketahui dalam contoh soal nilai mutlak di atas. Kurang lebih gambarnya seperti ini:

Anggaplah jarak sekolah ke toko buku adalah $x$, maka persamaan nilai mutlaknya adalah:

$|x-5|=1$

$(x-5)^2=1^2$

$x^2-10x+25=1$

$x^2-10x+24=0$

$(x-6)(x-4)=0$

Sehingga, diketahui kalau $x=6$ atau $x=4$. Artinya, jarak sekolah ke toko buku adalah 6 km atau 4 km dari sekolah.

Baca juga: Contoh Soal Pertidaksamaan Nilai Mutlak Lengkap dengan Pengertian, Sifat, dan Penerapannya

______________________________

Untuk kamu yang memiliki minat di bidang teknik, ilmu fisika, atau ekonomi, memahami aplikasi persamaan nilai mutlak akan sangat membantu kamu di masa depan. Karena itu, kamu bisa lebih banyak mencoba mengerjakan contoh soal nilai mutlak dan mencari contohnya dalam kehidupan sehari-hari mulai dari sekarang.

Bingung cari latihan soal tentang contoh soal nilai mutlak? Pijar Belajar solusinya! Kamu bisa mengakses ratusan hingga ribuan soal Matematika dan melatih kemampuanmu menghafal rumus! 

Yuk, berlangganan Pijar Belajar sekarang juga!